주제
Lesson 4: Counting Elements
난이도
Medium
문제
You are given N counters, initially set to 0, and you have two possible operations on them:
- increase(X) − counter X is increased by 1,
- max counter − all counters are set to the maximum value of any counter.
A non-empty array A of M integers is given. This array represents consecutive operations:
- if A[K] = X, such that 1 ≤ X ≤ N, then operation K is increase(X),
- if A[K] = N + 1 then operation K is max counter.
For example, given integer N = 5 and array A such that:
A[0] = 3
A[1] = 4
A[2] = 4
A[3] = 6
A[4] = 1
A[5] = 4
A[6] = 4
the values of the counters after each consecutive operation will be:
(0, 0, 1, 0, 0)
(0, 0, 1, 1, 0)
(0, 0, 1, 2, 0)
(2, 2, 2, 2, 2)
(3, 2, 2, 2, 2)
(3, 2, 2, 3, 2)
(3, 2, 2, 4, 2)
The goal is to calculate the value of every counter after all operations.
Write a function:
def solution(N, A)
that, given an integer N and a non-empty array A consisting of M integers, returns a sequence of integers representing the values of the counters.
Result array should be returned as an array of integers.
For example, given:
A[0] = 3
A[1] = 4
A[2] = 4
A[3] = 6
A[4] = 1
A[5] = 4
A[6] = 4
the function should return [3, 2, 2, 4, 2], as explained above.
Write an efficient algorithm for the following assumptions:
- N and M are integers within the range [1..100,000];
- each element of array A is an integer within the range [1..N + 1].
N 개의 카운터가 있고, 다 0부터 시작한다.
기능이 A라는 배열로 들어오는데, 만약 값이 X(1<=X<=N)이면 카운터 X를 +1해준다.
만약 값이 N+1이면 max counter라는 기능이 작동하는데, 이는 N개의 카운터 중 최대값으로 모든 카운터를 세팅하는 기능이다.
위의 작동 예시를 보면 쉽게 이해할 수 있다.
조건은 카운터 수 N과 배열의 크기 M은 1 ~ 100,000 사이의 값이며, A의 각각의 원소들은 1~N+1값만 갖는다.
풀이
역시나 efficient하게 풀라는 문제는 꼭 time complexity 때문에 timeout error를 만나줘야 직성이 풀린다!
그러므로 시간복잡도에 따라 두 개 다 풀이한다.
1. 시간복잡도 : O(M*N)
카운터의 횟수를 저장하기 위한 딕셔너리를 선언하고, 모든 카운터의 값을 0으로 초기화한다.
(딕셔너리의 key값이 카운터의 이름(1,2,...N)이고, value가 카운터의 수로 선언함.)
그 후 카운터 기능에 대한 배열 A의 모든 원소에 대해서 아래를 반복한다.
ⓐ 만약 기능 i가 N보다 크면(max counter), 딕셔너리 값 중에 최대값을 구하고, 그 값으로 딕셔너리를 다 업데이트한다.
ⓑ 그렇지 않다면 i를 key로 갖는 카운터의 value값을 +1한다. (해당 카운터 값을 +1한다.)
하지만 이럴 경우, 최대값을 구하기 위해서 쓴 max함수가 O(N), 최대값으로 다 업데이트할 때도 O(N)이여서 결국 총 시간복잡도는 O(M*N)이 된다. 그래서 ineifficient라 100점은 못 맞는다.
그러므로 위 로직에서는 max를 구하는 연산과 최대값으로 업데이트하는 부분을 최적화해야한다.
2. 시간복잡도 : O(M+N)
카운터의 횟수를 저장하기 위한 딕셔너리를 선언하고, 모든 카운터의 값을 0으로 초기화한다.
(딕셔너리의 key값이 카운터의 이름(1,2,...N)이고, value가 카운터의 수로 선언함.)
현재 진행 중인 카운터들의 최대값을 max_v라는 변수로, max counter 기능이 호출될 때의 max_v값을 update_max_v라고 하고, 각각 0으로 초기화시킨다.
그 후 카운터 기능에 대한 배열 A의 모든 원소에 대해서 아래를 반복한다.
ⓐ 만약 기능 i가 N보다 크면(max counter), update_max_v값을 max_v로 업데이트한다.
ⓑ 그렇지 않다면, 해당 카운터의 값이 update_max_v보다 작은지 확인후 작으면 update_max_v값으로 바꾼다.
(즉, max counter 기능이 호출된 직후 적용되는 것이 아니라, 여기서 작동된다.)
만약 카운터의 값이 update_max_v보다 크다면 이미 max counter기능이 적용되었거나 이미 max였던 카운터이므로 +1만 해준다.
마지막으로 해당 카운터의 값이 max_v보다 큰지 확인 후, 만약 크다면 max_v를 업데이트해준다.
(여기서 카운터들의 최대값을 계속 업데이트해준다.)
마지막으로 딕셔너리의 모든 value들을 확인하면서 update_max_v보다 작은 값들은 업데이트한다.
(즉, max counter가 적용안 된 value들은 마지막에 적용시켜준다.)
이럴 경우 max 함수도 쓰지 않았고, 딕셔너리 모든 값을 for문 중간에 업데이트를 하지 않아서 이중 for문도 피할 수 있다. 따라서 시간복잡도가 2차가 되지 않는다. 해당 로직의 예시는 아래 참고.
Ex. A = [3,4,4,6,1,4,4]
| i | max_v | update_max_v | counter 값 |
| 3 | 1 | 0 | (0, 0, 1, 0, 0) |
| 4 | 1 | 0 | (0, 0, 1, 1, 0) |
| 4 | 2 | 0 | (0, 0, 1, 2, 0) |
| 6 | 2 | 2 | (0, 0, 1, 2, 0) |
| 1 | 3 | 2 | (3, 0, 1, 2, 0) |
| 4 | 3 | 2 | (3, 0, 1, 3, 0) |
| 4 | 4 | 2 | (3, 0, 1, 4, 0) |
| - | 4 | 2 | (3, 2, 2, 4, 2) -> 리턴값 |
코드
- 시간복잡도 : O(M*N)
def solution_mn(N, A):
counter_dict = dict()
for i in range(1, N+1):
counter_dict[i] = 0
for i in A:
if i > N:
max_v = max(counter_dict.values()) # max func time complexity : O(N)
for i in range(1, N + 1):
counter_dict[i] = max_v
else:
counter_dict[i] += 1
return list(counter_dict.values())
- 시간 복잡도 : O(N+M)
# O(N+M)
def solution(N, A):
counter_dict = dict()
for i in range(1, N + 1):
counter_dict[i] = 0
# max value of counters (current/ongoing) time
# 현재 진행 중인 카운터들의 최대값(매번 확인해서 최댓값을 증가 및 유지)
max_v = 0
# max value when max counter operation is called
# max counter 함수가 불러와졌을 때 당시의 counter들의 최댓값으로, 추후에 counter들 연산 시 최소값으로 이용
# max counter 함수가 불러와진 이후에 max로 업데이트 시키기 위한 값이라 이해하면 될듯
update_max_v = 0
# O(M)
for i in A:
if i > N:
update_max_v = max_v
else:
if counter_dict[i] < update_max_v:
counter_dict[i] = update_max_v
counter_dict[i] += 1
# update max value instead of max func
if max_v < counter_dict[i]:
max_v = counter_dict[i]
# O(N)
for counter in counter_dict:
if counter_dict[counter] < update_max_v:
counter_dict[counter] = update_max_v
return list(counter_dict.values())
시간복잡도
정답인 마지막 코드를 기준으로,
첫번째 반복문 : O(M)
두번째 반복문 : O(N)
따라서 코드 전체의 복잡도는 O(M+N)이 된다.
결과
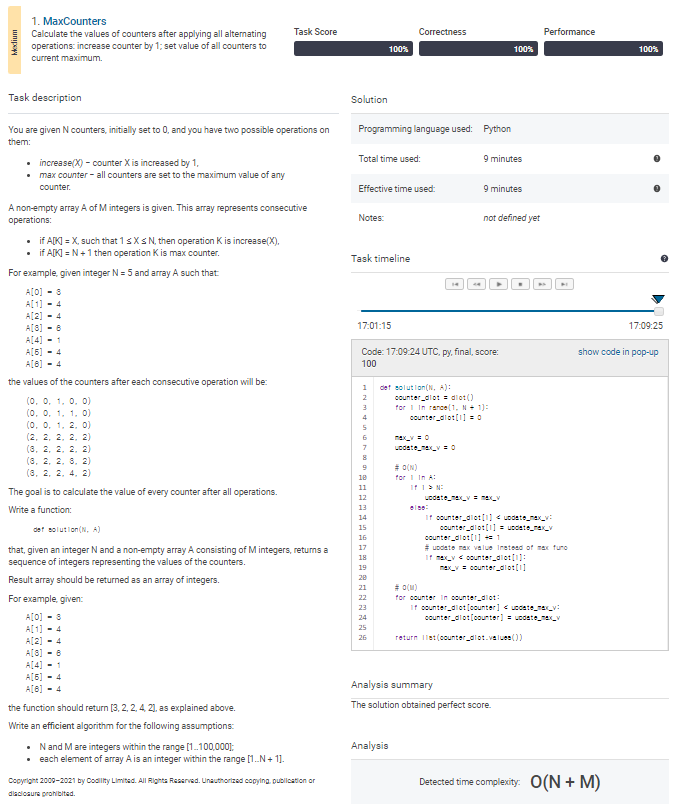
사진에는 9분이라 적혀있지만, 전체 과정 고려하면 1시간은 걸린 것 같다 ㅠㅠ
스스로 풀어서 뿌듯하지만 역시 너무 오래 걸린다...

'알고리즘 공부' 카테고리의 다른 글
| Codility: GenomicRangeQuery (Python) (0) | 2021.09.14 |
|---|---|
| Codility: CountDiv (Python) (0) | 2021.09.14 |
| Codility: PassingCars (Python) (0) | 2021.09.13 |
| Codility: PermCheck (Python) (0) | 2021.09.10 |
| Codility: MissingInteger (Python) (0) | 2021.09.10 |