본 게시물은 Qiskit의 게시글을 번역 및 추가한 게시물입니다.
양자 계산을 위한 선형대수학 -1 : 벡터는 이쪽으로!
본 문서에서 양자비트, Qubit에 대한 언급이 나옵니다. 행렬이 어떻게 적용되는지를 보여주기 위해 사용되는 것일뿐 이 챕터에서 중요한 부분이 아니기 때문에 혹시 양자비트에 대해 전혀 모르시는 분은 밑의 접힌 글을 읽어주세요.
우리가 현재 일반적으로 쓰는 컴퓨터(혹은 고전적인 컴퓨터, Classical Computer)는 0 혹은 1로 이루어진 bit들의 연산으로 돌아갑니다. 하지만 양자컴퓨터(Quantum Computer)는 일반적으로 우리가 알고있는 이진법으로는 표현이 불가능한 양자역학을 기반으로 만들어진 컴퓨터이기 때문에 Qubit라는 다른 개념을 가지고 연산을 합니다.
Qubit는 단순히 0 혹은 1로 딱 떨어지지 않으며, 0과 1의 확률로 표현이 됩니다. 이 확률을 Amplitude라고 표현합니다. 양자컴퓨터에서는 이 확률을 이용해서 구하려는 답을 찾기 때문에 매우 중요한 개념입니다.
대표적으로 이 챕터에서 등장할 Qubit을 보도록 하겠습니다.
$|0\rangle =$ $\left(\begin{array} {rr} 1 \\ 0 \end{array}\right) $, $|1\rangle =$ $\left(\begin{array} {rr} 0 \\ 1 \end{array}\right) $
입니다.
위처럼 Qubit는 Bra-Ket 표현을 사용해 표현이 가능하며, 혹은 행렬로도 표현이 가능합니다. 여기선 설명하지 않지만 Bloch Sphere라는 블로흐 구면으로도 표현이 가능합니다. 위의 두 상태는 1개의 Qubit을 이용해 표현한 양자 상태로
$|\theta\rangle =$ $\alpha|0\rangle + \beta|1\rangle = $ $\left(\begin{array} {rr} \alpha \\ \beta \end{array}\right) $
로 살펴볼 수 있으며 여기서 $\alpha$와 $\beta$는 각각 $\|0\rangle$과 $|1\rangle $의 확률입니다.
보다 더 자세한 설명은 Qiskit 1.3장이나 호롤리님의 Quantum bit부분을 읽으시면 도움이 될것입니다.
또한 본문에서 '고전적'이라고 표현하는 것은 Classical의 의미로, 현재 일반화되어 사용하고 있는 컴퓨터가 돌아가는 세계를 의미하며, '고전 물리학'과 '양자 물리학'에서 가져온 '고전'이라고 생각하시면 됩니다.
Matrices and Matrix Operations
앞서 본 벡터와 마찬가지로 행렬은 양자 알고리즘과 계산에 자주 사용이 됩니다.
여기서 행렬이란 벡터를 또 다른 벡터로 만드는 연산자입니다.
보통 행렬은 아래처럼 숫자의 배열처럼 나열이 됩니다.

행렬곱셈을 통해서 벡터에 행렬을 적용할 수 있습니다. 행렬곱셈은 두 개의 행렬에서 앞의 행렬의 n번째 '행'과 뒤의 행렬의 n번째 '열'을 곱해가면서 결과를 냅니다. 자세한 행렬 곱셈의 설명은 여기 혹은 아래의 예시를 봐주세요.
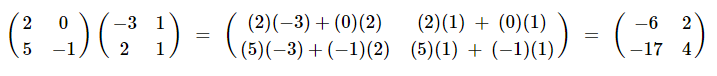
양자 계산을 하기 위해서는 양자 상태 벡터가 필요합니다. 이 벡터에 행렬을 곱함으로써 벡터를, 즉 양자 상태를 조작할 수 있습니다. 벡터는 하나의 열만 존재하는 행렬로 볼 수 있습니다. 따라서 벡터에 행렬을 적용하려면, 위의 행렬곱셈 과정을 따라하면 됩니다.
양자컴퓨터의 양자정보단위인 Qubit(큐비트)를 양자게이트를 차례대로 적용해서 조작할 수 있습니다. 그리고 각각의 양자 게이트는 행렬로 표현이 가능하기 때문에 상태 벡터에 적용이 가능하기 때문에 상태를 바꿀 수 있습니다. 예를 들어 대표적인 양자 게이트인 Pauli-X gate를 보도록 하겠습니다.

위 게이트가 Pauli-X gate며, 우리가 일반적으로 알고 있는 NOT 게이트와 유사합니다. $|0\rangle$를 $|1\rangle$로, $|1\rangle$를 $|0\rangle$로 바꿔줍니다. 즉, 상태를 뒤바꿔주는거죠. 그렇다면 양자 게이트가 어떻게 양자 상태 벡터에 적용이 되는지 확인해봅시다.

이렇게 상태 벡터에 행렬을 적용해서 변화를 줄 수 있습니다.
양자계산에서 중요한 행렬이 두가지가 있습니다. 바로 Hermitian 과 Unitary 행렬입니다.
Hermitian행렬은 양자기계학(Quantum Mechanics) 연구분야에서 더 중요하다면, Unitary 행렬은 양자기계학에서도 양자계산에서도 똑같이 중요합니다. 그렇기 때문에 Unitary 행렬은 꼭 이해하시길!
Hermitian 행렬은 켤레전치(conjugate transpose)를 한 행렬과 자기자신이 같은 행렬을 의미한다. 예를 들면 아래의 그림과 같습니다.
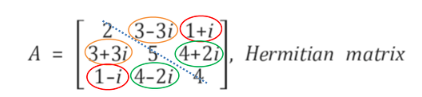
위처럼 대각선을 기준으로 했을 때, 서로 마주보고 있는 값들이 켤레복소수이며, 이를 켤레전치를 한다면 자기 자신과 같은 행렬이 될 것입니다. 여기서 켤레복소수나 전치행렬 개념을 모르겠다면 밑의 더보기를 클릭해주세요!
켤레복소수
$a+bi$ 형태로 무리수를 표현할 때, $a+bi$의 켤레복소수는 $a-bi$입니다. 즉, 실수부의 부호는 그대로 놔두고 허수부(i)의 부호만 바꾼 것을 켤레복소수라고 표현합니다.
전치(Transpose) 행렬
전치 행렬은 행과 열을 교환하여 얻는 행렬입니다.
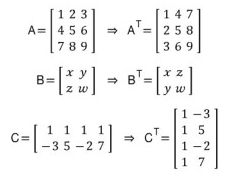
이는 다시 말해서 위 그림과 같은 주대각선(왼쪽 위부터 오른쪽 아래)을 축으로 하여 서로 대칭을 해서 얻게 되는 행렬입니다.
예를 들어서 Puali-Y gate를 행렬로 본다면 바로 이 Hermitian 행렬입니다. 밑에서 볼 수 있듯이 대각선을 기준으로 허수부의 부호를 바꿨을 때 다시 자기자신과 같아집니다. $\dagger$는 켤레전치를 의미하는 부호입니다.

Unitary 행렬은 역행렬(Inverse)이 켤레전치행렬(Conjugate transpose)과 같은 행렬을 의미합니다.

위와 같은 식으로 표현할 수 있는데, 여기서 단위행렬과 역행렬은 더보기를 참고하시기 바랍니다.
단위행렬 (Identity)
보통 $I$로 표현하며 행렬의 주대각선에는 1, 나머지는 다 0으로 채워진 행렬을 의미합니다. 어떠한 행렬에 단위행렬을 곱할경우 자기자신이 나옵니다.
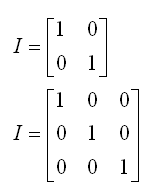
역행렬 (Inverse)
주어진 행렬에 곱해서 단위행렬로 만들 수 있는 행렬을 의미합니다. 주어진 행렬을 $A$라고 하면 역행렬은 $A^-1$로 표현합니다.
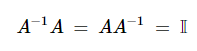
위처럼 표현할 수 있습니다.
Pauli-Y gate를 이용해서 다시 예시를 살펴본다면 다음과 같습니다.

위의 식을 살펴봄으로써 Pauli-Y gate는 Hermitian 행렬이자 Unitary 행렬임을 알 수 있습니다.
양자계산에서는 대게 Unitary 행렬을 다루기 때문에 역행렬은 주어진 것의 켤레전치를 하면 얻을 수 있습니다. Unitary 행렬의 경우에는 다음 챕터에서 다룰 힐버트 공간(Hilbert spaces)에서 중요성이 더욱 더 강조되며, 양자기계학의 세부주제로 많이 다뤄집니다. 여기서 주된 아이디어는 Unitary 행렬을 적용한 양자 상태의 진화가 양자 상태를 보존한다는 것입니다.
참고문헌
Qiskit : https://qiskit.org/textbook/ch-appendix/linear_algebra.html
Qubit와 양자 게이트 설명 : https://gruuuuu.github.io/quantum%20computing/quantum_gate/#
행렬식 : https://ratsgo.github.io/linear%20algebra/2017/05/21/determinants/
'정보보호 공부' 카테고리의 다른 글
| [악성코드] PE 파일(포맷) Part 2 - PE 파일 구조 (feat. 섹션) (0) | 2021.08.24 |
|---|---|
| 리소스 해커(Resource Hacker) 다운로드 및 사용법 (0) | 2021.08.24 |
| [악성코드] PE 파일(포맷) Part 2 - PE 파일 구조 (feat. IAT, 라이브러리) (0) | 2021.08.23 |
| [악성코드] PE 파일(포맷) Part 1 - 개념 및 생성과정과 구조 (0) | 2021.08.22 |
| 양자 계산을 위한 선형대수학 -1 : 벡터 (0) | 2020.07.06 |